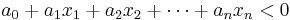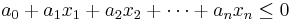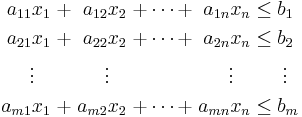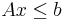Linear inequality
In mathematics a linear inequality is an inequality which involves a linear function.
Contents |
Linear inequalities in real numbers
Definitions
When two expressions are connected by 'greater than' or 'less than' sign, we get an inequation.
When operating in terms of real numbers, linear inequalities are the ones written in the forms
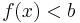 or
or 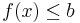 ,
,
where  is a linear functional in real numbers and b is a constant real number. Alternatively, these may be viewed as
is a linear functional in real numbers and b is a constant real number. Alternatively, these may be viewed as
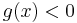 or
or 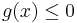 ,
,
where 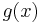 is an affine function.
is an affine function.
The above are commonly written out as
or
Sometimes they may be written out in the forms
or
Here 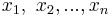 are called the unknowns,
are called the unknowns, 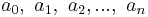 are called the coefficients, and
are called the coefficients, and  is the constant term.
is the constant term.
A linear inequality looks exactly like a linear equation, with the inequality sign replacing the equality sign.
A system of linear inequalities is a set of linear inequalities in the same variables:
Here 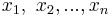 are the unknowns,
are the unknowns, 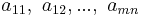 are the coefficients of the system, and
are the coefficients of the system, and 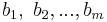 are the constant terms.
are the constant terms.
This can be concisely written as the matrix inequality:
where A is an m×n matrix, x is an n×1 column vector of variables, and b is an m×1 column vector of constants.
In the above systems both strict and non-strict inequalities may be used.
Not all systems of linear inequalities have solutions.
Interpretations and applications
The set of solutions of a real linear inequality constitutes a half-space of the n-dimensional real space, one of the two defined by the corresponding linear equation.
The set of solutions of a system of linear inequalities corresponds to the intersection of the half-planes defined by individual inequalities. It is a convex set, since the half-planes are convex sets, and the intersection of a set of convex sets is also convex. In the non-degenerate cases this convex set is a convex polyhedron (possibly unbounded, e.g., a half-space, a slab between two parallel half-spaces or a polyhedral cone). It may also be empty or a convex polyhedron of lower dimension confined to an affine subspace of the n-dimensional space Rn.
Sets of linear inequalities (called constraints) are used in the definition of linear programming.
Linear inequalities in terms of other mathematical objects
When you graph a linear inequality, it will be on one side of a line. Also, when you mark points where the line crosses where the x and y axis cross each other you can make the rise over run, which will help you find slope. If slope is denoted by m and y-intercept by b, you can find m = 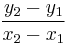 and b =
and b = 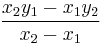 , so long as
, so long as 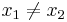 . Such line is described by the equation
. Such line is described by the equation 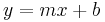 .
.
The above definition requires well-defined operations of addition, multiplication and comparison, therefore the notion of a linear inequality may be extended to ordered rings, in, particular, to ordered fields.